Nonlocal games and operator spaces: a survey

Over the past few months, together with Carlos Palazuelos I wrote a survey article on “Nonlocal Games and Operator Space Theory”, and we just uploaded it to the arXiv. The survey is an invited contribution to a special issue of JMP on Operator Algebras and Quantum Information Theory which will hopefully appear soon.

Exquisite(ly painful) memories

We had a lot of fun writing the survey. Teaming up with an expert in functional analysis behind probably more than half of the impressive range of results in quantum information theory that the “operator space approach” has so far led to gave me a great opportunity to solidify some of the mathematical material I have labored through in recent years.

It all started during a memorable summer of 2009 spent visiting Harry Buhrman’s group at CWI in Amsterdam. At the time the breakthrough by Perez-Garcia, Wolf, Palazuelos (yes, the same Palazuelos!), Villanueva and Junge demonstrating the existence of tripartite Bell inequalities with unbounded violation was all fresh. The result generated a lot of attention, first because it is a great and unexpected result (contrast with the fact that the maximum violation of bipartite inequalities is uniformly bounded, by Grothendieck’s constant), and second because the proof technique was completely novel, and seemed to rely crucially on “deep arguments from operator space theory”, a relatively young theory (barely younger than quantum information, but then time flows more slowly in mathematics) developed by operator algebraists starting with the work of Ruan in the late 1980s.

I spent probably a full month banging my head against the paper. After a month, I had gained a good grasp of just one thing: when they say deep arguments, they mean deep. Note the comment added for v2 of the paper on arXiv: “Substantial changes in the presentation to make the paper more accessible for a non-specialized reader”. You bet: that comment was already there in summer 2009, and I guarantee it didn’t make me feel any better! I printed the paper, borrowed all referenced books from the library, and tried. Then put it down, out of despair. Then tried again. Then put it down. Picked it up again. To the hell with it, put it down, tried to find my own proof. Failed. Back to the paper. It was a wild chase…I kept thinking I was starting to see how to go about things, only to fail — deeply.

Cutting a long story short, we did get a couple of things out of that summer. The paper by Perez-Garcia et al. [PGWPVJ] covers a lot of ground. The main result is an existential proof of a family of tripartite Bell correlation inequalities, or equivalently a family of three-player XOR games, such that the maximum advantage of quantum players sharing entanglement over classical players using only shared randomness, as measured by the ratio of the corresponding maximum biases (bias = deviation of acceptance probability from ${1/2}$ ), is unbounded: it grows with the size of the games. A second result proved in [PGWPVJ] is that achieving any unbounded violation requires the players to share a relatively complex entangled state: GHZ states ${|\psi\rangle= \frac{1}{\sqrt{d}} \sum_i |i\rangle|i\rangle|i\rangle}$ (of any dimension ${d}$ ), arguably a natural generalization of bipartite maximally entangled states, can only lead to a violation bounded by a universal constant.

After much suffering we were able to obtain generalizations and simplifications of both results — stripping out virtually all the operator space theory! First, with Jop Briet, Harry Buhrman and Troy Lee we extended the second result and showed that the maximum violation remains bounded for a larger class of states, including what we called “clique-wise entanglement” — combinations of EPR pairs, GHZ states, etc., as well as “Schmidt states”, states of the form ${|\psi\rangle = \sum_i \alpha_i |i\rangle|i\rangle|i\rangle}$ for arbitrary coefficients ${\alpha_i}$ . While this may seem innocuous, it turns out the extension to Schmidt states solves (via a reduction proved in [PGWPVJ]) an open question in operator algebras from the 1970s! The observation won us a fancy-sounding publication (“All Schatten spaces endowed with the Schur product are Q-algebras”) in a fancy-sounding journal (“Journal of Functional Analysis”). The result also has an interesting, completely classical consequence for the direct sum problem: it implies that there exists a three-player XOR game ${G}$ whose bias is bounded away from ${1}$ by a constant, but the bias of the XOR game obtained by taking the direct sum of ${k}$ copies of ${G}$ (the game is played ${k}$ times in parallel and the parity of all answers is checked against the correct parity) remains bounded away from ${0}$ , for all ${k}$ — a strong counterexample to parallel repetition (for the direct sum) of three-player games.

Second (and with a couple years’ more effort), with Jop Briet we managed to re-derive the main result of [PGWPVJ], again with some improvements: while still probabilistic our construction is explicit (we give a simple distribution on games such that the large violation holds with high probability), and the dependence of the violation on the game size as well as the entanglement dimension are greatly improved. Arguably our construction borrows its key ideas from whatever we could squeeze out of [PGWPVJ], but there are no more operator spaces! The most fancy tool used in the construction is a tail bound for second-order Gaussian chaos due to Latala.

The operator space connection

So, does operator space theory really provide a natural framework for the study of Bell inequalities, or does the heavy machinery systematically hide observations that could be obtained by easier means? While the range of results obtained by Perez-Garcia et al. using their techniques (including large violations for bipartite (non-XOR) inequalities and applications to quantum Shannon theory) seems to indicate that the tools are useful, it does not preclude that similar results could be obtained without having to resort to such high levels of obfuscation.

Since then I have grown more and more fond of the approach, to the point where I would in some cases agree that it provides the “right” point of view on a question about Bell inequalities (or nonlocal games) — a conclusion I would never have been able to reach without the invaluable help of David, Carlos, Marius, and my co-authors in these endeavors, Jop and Oded, whom I gratefully acknowledge! An example where I would say that the operator space viewpoint is undeniably the “right” one arises in work with Oded Regev on “Quantum XOR games” that grew out of our exploration of non-commutative extensions of Grothendieck’s inequality. For me a highlight of this work has been a derivation of the operator space Grothendieck inequality based on elementary techniques strongly inspired by the use of embezzlement states in quantum nonlocality.

These results, and many more, are described in the survey. While the JMP special issue is targeted at mathematicians, we tried to make the survey as self-contained as possible, and my hope is that it provides an easily approachable introduction to the delights of tensor norms, completely bounded maps and the associated “o.s.s.” for the interested quantum information theorist with little or no background in ${C^*}$ -algebras or operator space theory.

An example

I’d like to end with a bird’s-eye view of the operator space point of view on entangled games by taking an example from the survey, an upper bound on the largest possible ratio between the maximum success probabilities achievable by quantum entangled and classical players respectively in a two-player game, as a function of the number of answers per player in the game. For a formal treatment I refer to Proposition 4.5 in the survey; here I will stay at the level of symbols, hoping to carry some of the flavor across, but please keep in mind that the exposition below is not fully accurate.

Games as tensors and values as norms

The functional analytic approach views a game as a tensor ${G}$ on the space ${({\mathbb C}^N\otimes {\mathbb C}^K)\otimes ({\mathbb C}^N\otimes {\mathbb C}^K)}$ . Here ${N}$ and ${K}$ are respectively the number of questions and answers to and from each player, and each coefficient ${G_{x,y}^{a,b}}$ of the tensor corresponds to the associated payoff to the players in the game. The main thrust of the approach is that different value we are interested in — the classical value, or maximum success probability of classical players in the game, and the entangled value, or maximum success probability of quantum players sharing entanglement — are directly related to the norm of ${G}$ when the underlying spaces are normed in the appropriate way, as Banach spaces (for the classical value) or operator spaces (for the entangled value).

Let’s consider the classical value first. To capture it we’ll turn the vector space ${({\mathbb C}^N\otimes {\mathbb C}^K)\otimes ({\mathbb C}^N\otimes {\mathbb C}^K)}$ into the Banach space ${\ell_1^{N}(\ell_\infty^{K})\otimes_\epsilon \ell_1^{N}(\ell_\infty^{K})}$ . What does this mean? Let’s first focus on one of the factors, ${\ell_1^{N}(\ell_\infty^{K})}$ . We’re using the ${\ell_\infty}$ norm for the space ${{\mathbb C}^K}$ associated to answers, and the ${\ell_1}$ norm for the space ${{\mathbb C}^N}$ associated to questions. This choice is consistent with the interpretation of the game tensor as an object dual to the player’s strategies: glossing over considerations of non-negativity, a (classical) strategy is a collection of numbers ${\{f_x^a\}}$ such that

$\displaystyle \big\|\{f_x^a\}\big\|_{\ell_\infty^N(\ell_1^K)} = \max_x\,\sum_a |f_x^a| \leq 1.$

Once a norm has been defined on the spaces associated with each player’s strategy, it remains to put them together into a norm on the full game tensor, which lives on the tensor product of the two spaces. In general (including here) there will not be a unique way to norm the algebraic tensor product of two Banach spaces in a way that is consistent with the two Banach norms. (Indeed, the study of all possible such norms was pioneered by Grothendieck.) For our purposes it turns out that the smallest such norm, the injective norm ${\|\cdot\|_\epsilon}$ , is the right choice: the norm ${\|G\|_{\ell_1^{N}(\ell_\infty^{K})\otimes_\epsilon \ell_1^{N}(\ell_\infty^{K})}}$ exactly coincides with the maximum success probability of classical players in game ${G}$ . This is an easy calculation from the definition of the injective norm, but I’ll skip it here.

So that’s for classical strategies. Quantum strategies are a bit more complicated: instead of sequences of numbers ${\{f_x^a\}}$ they are represented by sequences of (positive semidefinite) matrices ${\{A_x^a\}}$ , of any dimension, such that ${\sum_a A_x^a = \mathbb{I}}$ for all ${x}$ . This is where operator spaces come in. An operator space is a structure that can be built on top of a Banach space by defining not just one norm but a sequence of matrix norms, on matrices of arbitrary dimension ${d=1,2,\ldots,}$ with entries in the Banach space. Here the most natural operator space structure on ${\ell_\infty^N(\ell_1^K)}$ replaces ${\ell_\infty^N}$ by ${M_N}$ ( ${N\times N}$ matrices with the operator norm) and ${\ell_1^K}$ by ${S_1^K}$ , whose operator space structure is a bit hard to define directly but can be obtained naturally via duality with ${M_K}$ ( ${S_1^K}$ does not correspond to the Schatten- ${1}$ norm; note that here we need an operator space, which provides much more structure than a Banach space). Once again I’ll skip the details: you’ll have to believe me that the resulting operator space structure, that I’ll continue writing as ${\ell_1^N(\ell_\infty^K)}$ , precisely captures the notion of quantum strategy, i.e. a family of POVMs. (The “precisely” here is somewhat blunt; in particular there are subtleties involved with e.g. dealing with the requirement that POVM elements be positive semidefinite, but it is possible to work around those.)

Next we need to norm the tensor product, again as an operator space. As it turns out, the injective norm that worked so well for classical strategies has a direct operator space analogue, the minimal norm, which perfectly captures the quantum value of the game tensor! (I won’t show why, but just as for the injective norm it’s a simple calculation from the definition.) I’ll write ${\|G\|_{\ell_1^{N}(\ell_\infty^{K})\otimes_{min} \ell_1^{N}(\ell_\infty^{K})}}$ for this norm, and from now on it’ll serve as a proxy for the entangled value of the game ${G}$ .

That’s a lot of “coincidences”, isn’t it? A norm on the tensor product of Banach spaces matches the classical value of a game tensor, while the natural operator space analogue of that norm matches the quantum value. Now you may start to see why someone well-versed in the theory of such norms might see them as the “right” way to look at classical, and quantum, strategies. More details on this point in Section 2 of the survey.

A bound on the largest violation

But let’s move on. With the basic normed spaces in place the task of relating the classical and entangled values of a game can be formulated as follows: it amounts to estimating the norm of the identity map (as an aside, almost all results in functional analysis, or at least those that connect to the study of nonlocal games, that I have encountered seem to reduce to studying the “norm of the identity”… a fact that still makes me smile every time I stumble upon it: why isn’t the identity trivial?)

$\displaystyle id:\,\ell_1^{N}(\ell_\infty^{K})\otimes_{\epsilon} \ell_1^{N}(\ell_\infty^{K})\rightarrow \ell_1^{N}(\ell_\infty^{K})\otimes_{min} \ell_1^{N}(\ell_\infty^{K}).$

Indeed, as we have seen the norm of the game tensor when seen as an object on the first space corresponds to its classical value, while the norm of the same tensor considered as an object on the second space matches its entangled value. Any upper bound on the norm on the identity is an upper bound on the largest (multiplicative) advantage that can be gained by quantum players, while any lower bound will imply the existence of a game for which the advantage can be just as large.

Our strategy for bounding the norm of ${id}$ is to decompose it as a sequence of three simpler maps, on which it is easy to obtain norm estimates. We’ll start from the right-hand side, and consider first the arrow

$\displaystyle \ell_1^{NK}\otimes_{min} \ell_1^{NK}\rightarrow \ell_1^{N}(\ell_\infty^{K})\otimes_{min} \ell_1^{N}(\ell_\infty^{K}).$

If the map is taken to be the identity, the condition ${\max_{x} \|\sum_a A_x^a\|\leq 1}$ only gives us ${\max_{x,a} \|\sum_a A_x^a\|\leq 1}$ , thus the norm of the identity is ${1}$ . We can do better: consider the Fourier transform

$\displaystyle \mathcal{F}: \,\{A_{x}^a\}_{x,a}\mapsto \Big\{ E_{x,k} = \frac{1}{\sqrt{K}}\sum_a e^{\frac{-2i\pi ka}{K}} A_{x}^a\Big\}_k, x=1,\ldots,N.$

It is not hard to verify that if for every ${x}$ , ${\{A_x^a\}_a}$ is a POVM then for every ${x,k}$ it will hold that ${\| E_{x,k} \|\leq K^{-1/2}}$ : accounting for both players we saved a factor ${K^{-1}}$ .

The next arrow we consider is

$\displaystyle \ell_1^{NK}\otimes_{\epsilon} \ell_1^{NK}\rightarrow \ell_1^{NK}\otimes_{min} \ell_1^{NK}.$

This is a key step: we are switching from the ${\epsilon}$ to the ${min}$ norm, from classical to quantum. But note how now the spaces are just ${\ell_1}$ : only questions, no answers — but there are signs, and what we are looking at is precisely the setting of XOR games, i.e. Grothendieck’s inequality! Therefore for this map we can simply take the identity, and its norm will be at most Grothendieck’s constant ${K_G}$ .

Finally, for the last arrow we consider

$\displaystyle \ell_1^{N}(\ell_\infty^{K})\otimes_{\epsilon} \ell_1^{N}(\ell_\infty^{K})\rightarrow \ell_1^{NK}\otimes_{\epsilon} \ell_1^{NK}.$

In order for the three arrows to compose to ${id}$ we should take this map to be the inverse of the Fourier transform ${\mathcal{F}}$ used in the first step. But note that now we are working with the ${\epsilon}$ norm, or in other words classical strategies. Thus it suffices to bound

$\displaystyle {\max_x\sum_a K^{-1/2}|\sum_{k} e^{\frac{2i\pi ak}{K}} t_{x,k}|}$

for ${t_{x,k}}$ such that ${\max_{x,k} |t_{x,k}|\leq 1}$ , and by Parseval this is easily seen to be at most ${K}$ . Hence our first map has norm ${K^2}$ .

There we are! We managed to write the identity ${id}$ , which maps the game tensor from an object acting on classical strategies to one acting on quantum strategies, as the composition of three maps with norms at most ${K^2}$ , ${K_G}$ and ${K^{-1}}$ respectively. As a direct consequence, we’ve proven that the largest violation achievable by quantum strategies is at most ${K_G\cdot K}$ , i.e. it is at most a constant times the number of possible answers in the game (warning: some constant factors missing, from e.g. glossing over complex vs real vs non-negative issues in the above).

What I like about this proof is that, from the point of view of operator spaces the above sketch is very natural (at least if I am to believe Carlos…), almost an exercise: as already mentioned, estimating the norm of the identity from one space to the other is the bread and butter of functional analysts, and they certainly have more than one trick up their sleeve. Unwinding the argument to frame it as a rounding procedure that transforms quantum entangled strategies into classical ones reveals some surprising tricks (e.g. the Fourier transform, which is used here to perform the actual quantum-to-classical rounding at the optimal step, the middle arrow) that one might not have thought of based solely on the usual “quantum toolbox”.

I’ll refer you to the survey for much more! All comments are very welcome and much appreciated; even typos: there is still plenty of time to fix those before the survey makes its way to the JMP presses.

3 Responses to Nonlocal games and operator spaces: a survey

Jon Awbrey says:

December 2, 2015 at 3:48 am

Doesn’t look like WP LaTeX has a \ket function, would have to use something like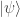 $|\psi\rangle$

- Thomas says:
  
  December 2, 2015 at 4:01 am
  
  Thanks — fixed.
  
Henry Yuen says:

December 2, 2015 at 8:15 pm

This reminds me of a talk given by JM Landsberg on the complexity of matrix multiplication. At one point he said, if viewed correctly, all our questions about the matrix multiplication tensor boils down to understanding the rank of the identity tensor (!). What’s so hard about the identity tensor? I still don’t quite believe it, but here the identity map seems to again play a nontrivial role.