[7/9/17 Update: Following a suggestion by Oded Regev I upgraded Section 1 from “probabilistic functions” to “matrix-valued functions”. This hopefully makes it a more useful, and interesting, mid-point between the classical analysis of BLR and the non-abelian extension discussed afterwards. I also fixed a bunch of typos — I apologize for the many remaining ones. The pdf has also been fixed.]
Last week Anand Natarajan from MIT presented our joint work on “A Quantum Linearity Test for Robustly Verifying Entanglement” at the STOC’17 conference in Montreal. Since we first posted our paper on the quant-ph arXiv, Anand and I discovered that the test and its analysis could be reformulated in a more general framework of tests for group relations, and rounding of approximate group representations to exact group representations. This reformulation is stimulated by a beautiful paper by Gowers and Hatami on “Inverse and stability theorems for approximate representations of finite groups”, which was first pointed to me by William Slofstra. The purpose of this post is to present the Gowers-Hatami result as a natural extension of the Blum-Luby-Rubinfeld linearity test to the non-abelian setting, with application to entanglement testing. (Of course Gowers and Hatami are well aware of this — though maybe not of the application to entanglement tests!) My hope in doing so is to make our result more accessible, and hopefully draw some of my readers from theoretical computer science into a beautiful area.
I will strive to make the post self-contained and accessible, with no quantum information background required — indeed, most of the content is purely — dare I say elegantly — mathematical. In the interest of being precise (and working out better parameters for our result than appear in our paper) I include essentially full proofs, though I may allow myself to skip a line or two in some of the calculations.
Given the post remains rather equation-heavy, here is a pdf with the same contents; it may be more convenient to read.
I am grateful to Anand, and Oded Regev and John Wright, for helpful comments on a preliminary version of this post.
1. Linearity testing
The Blum-Luby-Rubinfeld linearity test provides a means to certify that a function 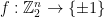 is close to a linear function. The test can be formulated as a two-player game:
is close to a linear function. The test can be formulated as a two-player game:
BLR linearity test:
- (a) The referee selects
 uniformly at random. He sends the pair
uniformly at random. He sends the pair  to one player, and either
to one player, and either  ,
,  , or
, or 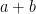 (chosen uniformly at random) to the other.
(chosen uniformly at random) to the other.
- (b) The first player replies with two bits, and the second player with a single bit. The referee accepts if and only if the player’s answers satisfy the natural consistency constraint.
This test, as all others considered here, treats both players symmetrically. This allows us to restrict our attention to the case of players who both apply the same strategy, an assumption I will systematically make from now on.
Blum et al.’s result states that any strategy for the players in the linearity test must provide answers chosen according to a function that is close to linear. In this section I will provide a slight “matrix-valued” extension of the BLR result, that follows almost directly from the usual Fourier-analytic proof but will help clarify the extension to the non-abelian case.
1.1. Matrix-valued strategies
The “classical” analysis of the BLR test starts by modeling an arbitrary strategy for the players as a pair of functions 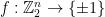 (for the second player, who receives a single string as query) and
(for the second player, who receives a single string as query) and  (for the first player, who receives a pair of strings as query). In doing so we are making an assumption: that the players are deterministic. More generally, we should allow “probabilistic strategies”, which can be modeled via “probabilistic functions”
(for the first player, who receives a pair of strings as query). In doing so we are making an assumption: that the players are deterministic. More generally, we should allow “probabilistic strategies”, which can be modeled via “probabilistic functions”  and
and 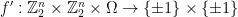 respectively, where
respectively, where 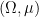 is an arbitrary probability space which plays the role of shared randomness between the players. Note that the usual claim that “probabilistic strategies are irrelevant because they can succeed no better than deterministic strategies” is somewhat moot here: the point is not to investigate success probabilities — it is easy to pass the BLR test with probability
is an arbitrary probability space which plays the role of shared randomness between the players. Note that the usual claim that “probabilistic strategies are irrelevant because they can succeed no better than deterministic strategies” is somewhat moot here: the point is not to investigate success probabilities — it is easy to pass the BLR test with probability  — but rather derive structural consequences from the assumption that a certain strategy passes the test. In this respect, enlarging the kinds of strategies we consider valid can shed new light on the strengths, and weaknesses, of the test.
— but rather derive structural consequences from the assumption that a certain strategy passes the test. In this respect, enlarging the kinds of strategies we consider valid can shed new light on the strengths, and weaknesses, of the test.
Thus, and with an eye towards the “quantum” analysis to come, let us consider an even broader set of strategies, which I’ll refer to as “matrix-valued” strategies. A natural matrix-valued analogue of a function  is
is  , where
, where 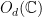 is the set of
is the set of 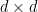 Hermitian matrices that square to identity (equivalently, have all eigenvalues in
Hermitian matrices that square to identity (equivalently, have all eigenvalues in 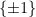 ); these matrices are called “observables” in quantum mechanics. Similarly, we may generalize a function
); these matrices are called “observables” in quantum mechanics. Similarly, we may generalize a function  to a function
to a function 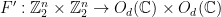 . Here we’ll impose an additional requirement: any pair
. Here we’ll impose an additional requirement: any pair 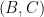 in the range of
in the range of 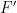 should be such that
should be such that 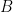 and
and 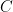 commute. The latter condition is important so that we can make sense of the function as a strategy for the provers: we should be able to ascribe a probability distribution on outcomes
commute. The latter condition is important so that we can make sense of the function as a strategy for the provers: we should be able to ascribe a probability distribution on outcomes  to any query
to any query  sent to the players. This is achieved by defining
sent to the players. This is achieved by defining
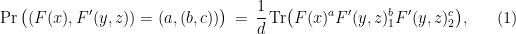
where for any observable  we denote
we denote 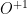 and
and  the projections on the
the projections on the 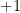 and
and 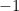 eigenspaces of
eigenspaces of  , respectively (so
, respectively (so  and
and  ). The condition that
). The condition that 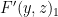 and
and 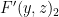 commute ensures that this expression is always non-negative; moreover it is easy to check that for all
commute ensures that this expression is always non-negative; moreover it is easy to check that for all  it specifies a well-defined probability distribution on
it specifies a well-defined probability distribution on 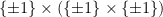 . Observe also that in case
. Observe also that in case 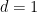 we recover the classical deterministic case, for which with our notation
we recover the classical deterministic case, for which with our notation 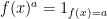 . If all
. If all 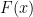 and
and  are simultaneously diagonal matrices we recover the probabilistic case, with the role of
are simultaneously diagonal matrices we recover the probabilistic case, with the role of 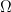 (the shared randomness) played by the rows of the matrices (hence the normalization of
(the shared randomness) played by the rows of the matrices (hence the normalization of 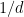 ; we will see later how to incorporate the use of non-uniform weights).
; we will see later how to incorporate the use of non-uniform weights).
With these notions in place we establish the following simple lemma, which states the only consequence of the BLR test we will need.
Lemma 1 Let  be an integer,
be an integer,  , and
, and  and
and 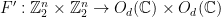 a matrix strategy for the BLR test, such that players determining their answers according to this strategy (specifically, according to (1)) succeed in the test with probability at least
a matrix strategy for the BLR test, such that players determining their answers according to this strategy (specifically, according to (1)) succeed in the test with probability at least 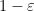 . Then
. Then
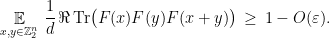
Introducing a normalized inner product 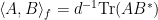 on the space of
on the space of 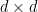 matrices with complex entries (the
matrices with complex entries (the  designates the conjugate-transpose), the conclusion of the lemma is that
designates the conjugate-transpose), the conclusion of the lemma is that  .
.
Proof: Success with probability 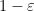 in the test implies the three conditions
in the test implies the three conditions
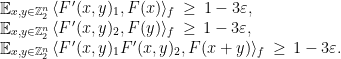
To conclude, use the triangle inequality as
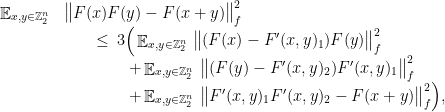
where 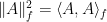 denotes the dimension-normalized Frobenius norm. Expanding each squared norm and using the preceding conditions and
denotes the dimension-normalized Frobenius norm. Expanding each squared norm and using the preceding conditions and 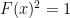 for all
for all  proves the lemma.
proves the lemma. 
1.2. The BLR theorem for matrix-valued strategies
Before stating a BLR theorem for matrix-valued strategies we need to define what it means for such a function  to be linear. Consider first the case of probabilistic functions, i.e.
to be linear. Consider first the case of probabilistic functions, i.e.  such that all
such that all 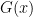 are diagonal, in the same basis. Any such
are diagonal, in the same basis. Any such  whose every diagonal entry is of the form
whose every diagonal entry is of the form 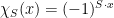 for some
for some  which may depend on the row/column number will pass the BLR test. This shows that we cannot hope to force
which may depend on the row/column number will pass the BLR test. This shows that we cannot hope to force  to be a single linear function, we must allow “mixtures”. Formally, call
to be a single linear function, we must allow “mixtures”. Formally, call  linear if
linear if  for some decomposition
for some decomposition  of the identity, i.e. the
of the identity, i.e. the 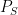 are pairwsie orthogonal projections such that
are pairwsie orthogonal projections such that 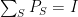 . Note that this indeed captures the probabilistic case; in fact, up to a basis change it is essentially equivalent to it. Thus the following may come as a surprise.
. Note that this indeed captures the probabilistic case; in fact, up to a basis change it is essentially equivalent to it. Thus the following may come as a surprise.
Theorem 2 Let  be an integer,
be an integer,  , and
, and  such that
such that
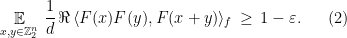
Then there exists a  , an isometry
, an isometry 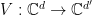 , and a linear
, and a linear  such that
such that
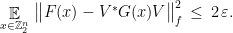
Note the role of 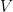 here, and the lack of control on
here, and the lack of control on 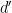 (more on both aspects later). Even if
(more on both aspects later). Even if  is a deterministic function
is a deterministic function  , i.e.
, i.e. 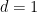 , the function
, the function  returned by the theorem may be matrix-valued. In this case the isometry
returned by the theorem may be matrix-valued. In this case the isometry 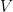 is simply a unit vector
is simply a unit vector  , and expanding out the squared norm in the conclusion of the theorem yields the equivalent conclusion
, and expanding out the squared norm in the conclusion of the theorem yields the equivalent conclusion
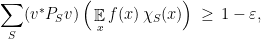
where we expanded  using our definition of a linear matrix-valued function. Note that
using our definition of a linear matrix-valued function. Note that 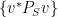 defines a probability distribution on
defines a probability distribution on 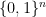 . Thus by an averaging argument there must exist an
. Thus by an averaging argument there must exist an  such that
such that  for a fraction at least
for a fraction at least 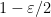 of all
of all  : the usual conclusion of the BLR theorem is recovered.
: the usual conclusion of the BLR theorem is recovered.
Proof: The proof of the theorem follows the classic Fourier-analytic proof of Bellare et al. Our first step is to define the isometry 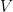 . For a vector
. For a vector 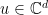 , define
, define
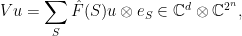
where  is the matrix-valued Fourier coefficient of
is the matrix-valued Fourier coefficient of  at
at  and
and  an arbitrary orthonormal basis of
an arbitrary orthonormal basis of  . An easily verified extension of Parseval’s formula shows
. An easily verified extension of Parseval’s formula shows 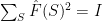 (recall
(recall  for all
for all  ), so that
), so that 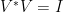 :
: 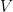 is indeed an isometry.
is indeed an isometry.
Next, define the linear probabilistic function  by
by  , where
, where 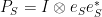 forms a partition of identity. We can evaluate
forms a partition of identity. We can evaluate
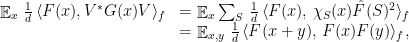
where the last equality follows by expanding the Fourier coefficients and noticing the appropriate cancellation. Together with (2), this proves the theorem. 
At the risk of sounding yet more pedantic, it might be useful to comment on the relation between this proof and the usual argument. The main observation in Bellare et al.’s proof is that approximate linearity, expressed by (2), implies a lower bound on the sum of the cubes of the Fourier coefficients of  . Together with Parseval’s formula, this bound implies the existence of a large Fourier coefficient, which identifies a close-by linear function.
. Together with Parseval’s formula, this bound implies the existence of a large Fourier coefficient, which identifies a close-by linear function.
The proof I gave decouples the argument. Its first step, the construction of the isometry 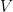 depends on
depends on  , but does not use anything regarding approximate linearity. It only uses Parseval’s formula to argue that the isometry is well-defined. A noteworthy feature of this step is that the function
, but does not use anything regarding approximate linearity. It only uses Parseval’s formula to argue that the isometry is well-defined. A noteworthy feature of this step is that the function  on the extended space is always well-defined as well: given a function
on the extended space is always well-defined as well: given a function  , it is always possible to consider the linear matrix-valued function which “samples
, it is always possible to consider the linear matrix-valued function which “samples  according to
according to  ” and then returns
” and then returns 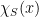 . The second step of the proof evaluates the correlation of
. The second step of the proof evaluates the correlation of  with the “pull-back” of
with the “pull-back” of  , and observes that this correlation is precisely our measure of “approximate linearity” of
, and observes that this correlation is precisely our measure of “approximate linearity” of  , concluding the proof without having had to explicitly notice that there existed a large Fourier coefficient.
, concluding the proof without having had to explicitly notice that there existed a large Fourier coefficient.
1.3. The group-theoretic perspective
Let’s re-interpret the proof we just gave using group-theoretic language. A linear function 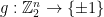 is, by definition, a mapping which respects the additive group structure on
is, by definition, a mapping which respects the additive group structure on 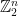 , namely it is a representation. Since
, namely it is a representation. Since 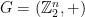 is an abelian group, it has
is an abelian group, it has  irreducible
irreducible  -dimensional representations, given by the characters
-dimensional representations, given by the characters  . As such, the linear function defined in the proof of Theorem 2 is nothing but a list of all irreducible representations of
. As such, the linear function defined in the proof of Theorem 2 is nothing but a list of all irreducible representations of  .
.
The condition (2) derived in the proof of the theorem can be interpreted as the condition that  is an “approximate representation” of
is an “approximate representation” of  . Let’s make this a general definition. For
. Let’s make this a general definition. For  -dimensional matrices
-dimensional matrices 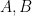 and
and  such that
such that  is positive semidefinite, write
is positive semidefinite, write
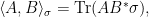
where we use 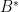 to denote the conjugate-transpose. The following definition considers arbitrary finite groups (not necessarily abelian).
to denote the conjugate-transpose. The following definition considers arbitrary finite groups (not necessarily abelian).
Definition 3 Given a finite group  , an integer
, an integer  ,
,  , and a
, and a  -dimensional positive semidefinite matrix
-dimensional positive semidefinite matrix  with trace
with trace  , an
, an 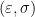 -representation of
-representation of  is a function
is a function 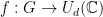 , the unitary group of
, the unitary group of 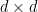 matrices, such that
matrices, such that
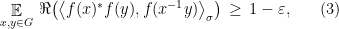
where the expectation is taken under the uniform distribution over  .
.
The condition (3) in the definition is very closely related to Gowers’s 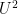 norm
norm
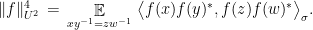
While a large Gowers norm implies closeness to an affine function, we are interested in testing linear functions, and the condition (3) will arise naturally from our calculations in the next section.
If 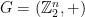 , the product
, the product 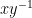 should be written additively as
should be written additively as 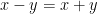 , so that the condition (2) is precisely that
, so that the condition (2) is precisely that  is an
is an 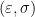 -representation of
-representation of  , where
, where 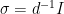 . Theorem 2 can thus be reformulated as stating that for any
. Theorem 2 can thus be reformulated as stating that for any 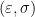 -approximate representation of the abelian group
-approximate representation of the abelian group 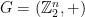 there exists an isometry
there exists an isometry  and an exact representation
and an exact representation 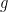 of
of  on
on 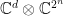 such that
such that  is well-approximated by the “pull-back”
is well-approximated by the “pull-back”  of
of 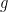 to
to 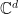 . In the next section I will make the words in quotes precise and generalize the result to the case of arbitrary finite groups.
. In the next section I will make the words in quotes precise and generalize the result to the case of arbitrary finite groups.
2. Approximate representations of non-abelian groups
2.1. The Gowers-Hatami theorem
In their paper Gowers and Hatami consider the problem of “rounding” approximate group representations to exact representations. I highly recommend the paper, which gives a thorough introduction to the topic, including multiple motivations. Here I will state and prove a slightly more general, but quantitatively weaker, variant of their result inspired by the somewhat convoluted analysis of the BLR test given in the previous section.
Theorem 4 (Gowers-Hatami) Let  be a finite group,
be a finite group,  , and
, and  an
an 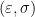 -representation of
-representation of  . Then there exists a
. Then there exists a  , an isometry
, an isometry 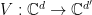 , and a representation
, and a representation  such that
such that
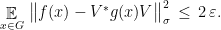
Gowers and Hatami limit themselves to the case of  , which corresponds to the dimension-normalized Frobenius norm. In this scenario they in addition obtain a tight control of the dimension
, which corresponds to the dimension-normalized Frobenius norm. In this scenario they in addition obtain a tight control of the dimension 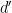 , and show that one can always take
, and show that one can always take  in the theorem. I will give a much shorter proof than theirs (the proof is implicit in their argument) that does not seem to allow to recover this estimate. (It is possible to adapt their proof to keep a control of
in the theorem. I will give a much shorter proof than theirs (the proof is implicit in their argument) that does not seem to allow to recover this estimate. (It is possible to adapt their proof to keep a control of 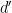 even in the case of general
even in the case of general  , but I will not explain this here.) Essentially the same proof as the one sketched below has been extended to some classes of infinite groups by De Chiffre, Ozawa and Thom in a recent preprint.
, but I will not explain this here.) Essentially the same proof as the one sketched below has been extended to some classes of infinite groups by De Chiffre, Ozawa and Thom in a recent preprint.
Note that, contrary to the BLR theorem, where the “embedding” is not strictly necessary (if  is small enough we can identify a single close-by linear function), as noted by Gowers and Hatami Theorem 4 does not in general hold with
is small enough we can identify a single close-by linear function), as noted by Gowers and Hatami Theorem 4 does not in general hold with 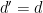 . The reason is that it is possible for
. The reason is that it is possible for  to have an approximate representation in some dimension
to have an approximate representation in some dimension  , but no exact representation of the same dimension: to obtain an example of this, take any group
, but no exact representation of the same dimension: to obtain an example of this, take any group  that has all non-trivial irreducible representations of large enough dimension, and create an approximate representation in e.g. dimension one less by “cutting off” one row and column from an exact representation. The dimension normalization induced by the norm
that has all non-trivial irreducible representations of large enough dimension, and create an approximate representation in e.g. dimension one less by “cutting off” one row and column from an exact representation. The dimension normalization induced by the norm 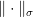 will barely notice this, but it will be impossible to “round” the approximate representation obtained to an exact one without modifying the dimension.
will barely notice this, but it will be impossible to “round” the approximate representation obtained to an exact one without modifying the dimension.
The necessity for the embedding helps distinguish the Gowers-Hatami result from other extensions of the linearity test to the non-abelian setting, such as the work by Ben-Or et al. on non-Abelian homomorphism testing (I thank Oded Regev for pointing me to the paper). In that paper the authors show that a function 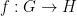 , where
, where  and
and  are finite non-abelian groups, which satisfies
are finite non-abelian groups, which satisfies 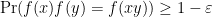 , is
, is 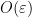 -close to a homomorphism
-close to a homomorphism 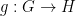 . The main difference with the setting for the Gowers-Hatami result is that since
. The main difference with the setting for the Gowers-Hatami result is that since  is finite, Ben-Or et al. use the Kronecker
is finite, Ben-Or et al. use the Kronecker 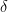 function as distance on
function as distance on  . This allows them to employ combinatorial arguments, and provide a rounding procedure that does not need to modify the range space (
. This allows them to employ combinatorial arguments, and provide a rounding procedure that does not need to modify the range space ( ). In contrast, here the unitary group is infinite.
). In contrast, here the unitary group is infinite.
The main ingredient needed to extend the analysis of the BLR test is an appropriate notion of Fourier transform over non-abelian groups. Given an irreducible representation 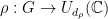 , define
, define
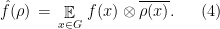
In case  is abelian, we always have
is abelian, we always have 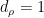 , the tensor product is a product, and (4) reduces to the usual definition of Fourier coefficient. The only properties we will need of irreducible representations is that they satisfy the relation
, the tensor product is a product, and (4) reduces to the usual definition of Fourier coefficient. The only properties we will need of irreducible representations is that they satisfy the relation
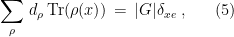
for any  . Note that plugging in
. Note that plugging in  (the identity element in
(the identity element in  ) yields
) yields  .
.
Proof: } As in the proof of Theorem 2 our first step is to define an isometry 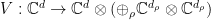 by
by
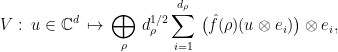
where the direct sum ranges over all irreducible representations 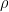 of
of  and
and 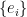 is the canonical basis. Note what
is the canonical basis. Note what 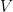 does: it “embeds” any vector
does: it “embeds” any vector 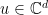 into a direct sum, over irreducible representations
into a direct sum, over irreducible representations 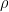 , of a
, of a  -dimensional vector of
-dimensional vector of 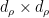 matrices. Each (matrix) entry of this vector can be thought of as the Fourier coefficient of the corresponding entry of the vector
matrices. Each (matrix) entry of this vector can be thought of as the Fourier coefficient of the corresponding entry of the vector  associated with
associated with 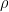 . If
. If  and
and  ranges over
ranges over  this recovers the isometry defined in the proof of Theorem 2. And indeed, the fact that
this recovers the isometry defined in the proof of Theorem 2. And indeed, the fact that 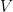 is an isometry again follows from the appropriate extension of Parseval’s formula:
is an isometry again follows from the appropriate extension of Parseval’s formula:
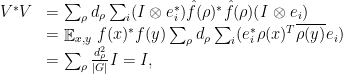
where for the second line we used the definition (4) of 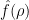 and for the third we used (5) and the fact that
and for the third we used (5) and the fact that  takes values in the unitary group.
takes values in the unitary group.
Following the same steps as in the proof of Theorem 2, we next define
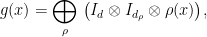
a direct sum over all irreducible representations of  (hence itself a representation). Lets’ first compute the “pull-back” of
(hence itself a representation). Lets’ first compute the “pull-back” of 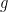 by
by 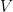 : following a similar calculation as above, for any
: following a similar calculation as above, for any  ,
,
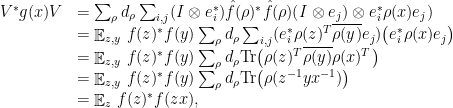
where the last equality uses (5). It then follows that
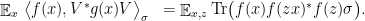
This relates correlation of  with
with  to the quality of
to the quality of  as an approximate representation and proves the theorem.
as an approximate representation and proves the theorem. 
2.2. Application: the Weyl-Heisenberg group
In quantum information we care a lot about the Pauli group. For our purposes it will be be sufficient (and much more convenient, allowing us to avoid some trouble with complex conjugation) to consider the Weyl-Heisenberg group  , or “Pauli group modulo complex conjugation”, which is the
, or “Pauli group modulo complex conjugation”, which is the  -element group
-element group  whose multiplication table matches that of the
whose multiplication table matches that of the 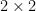 matrices
matrices
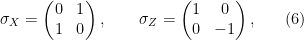
 and
and 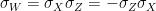 . This group has four
. This group has four  -dimensional representations, uniquely specified by the image of
-dimensional representations, uniquely specified by the image of  and
and  in
in 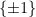 , and a single irreducible
, and a single irreducible  -dimensional representation, given by the matrices defined above. We can also consider the “
-dimensional representation, given by the matrices defined above. We can also consider the “ -qubit Weyl-Heisenberg group”
-qubit Weyl-Heisenberg group” 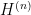 , the matrix group generated by
, the matrix group generated by  -fold tensor products of the
-fold tensor products of the 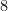 matrices identified above. The irreducible representations of
matrices identified above. The irreducible representations of 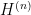 are easily computed from those of
are easily computed from those of  ; for us the only thing that matters is that the only irreducible representation which satisfies
; for us the only thing that matters is that the only irreducible representation which satisfies  has dimension
has dimension  and is given by the defining matrix representation (in fact, it is the only irreducible representation in dimension larger than
and is given by the defining matrix representation (in fact, it is the only irreducible representation in dimension larger than  ).
).
With the upcoming application to entanglement testing in mind, I will state a version of Theorem 4 tailored to the group 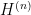 and a specific choice of presentation for the group relations. Towards this we first need to recall the notion of Schmidt decomposition of a bipartite state (i.e. unit vector)
and a specific choice of presentation for the group relations. Towards this we first need to recall the notion of Schmidt decomposition of a bipartite state (i.e. unit vector) 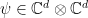 . The Schmidt decomposition states that any such vector can be written as
. The Schmidt decomposition states that any such vector can be written as
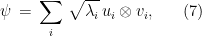
for some orthonomal bases 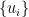 and
and 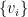 of
of 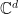 (the “Schmidt vectors”) and non-negative coefficients
(the “Schmidt vectors”) and non-negative coefficients 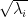 (the “Schmidt coefficients”). The decomposition can be obtained by “reshaping”
(the “Schmidt coefficients”). The decomposition can be obtained by “reshaping”  into a
into a 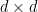 matrix
matrix 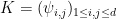 and performing the singular value decomposition. To
and performing the singular value decomposition. To 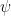 we associate the (uniquely defined) positive semidefinite matrix
we associate the (uniquely defined) positive semidefinite matrix
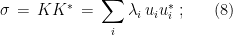
note that  has trace
has trace  . The matrix
. The matrix  is called the reduced density of
is called the reduced density of 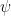 (on the first system).
(on the first system).
Corollary 5 Let 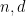 be integer,
be integer, 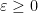 ,
, 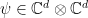 a unit vector,
a unit vector,  the positive semidefinite matrix associated to
the positive semidefinite matrix associated to 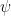 as in (8), and
as in (8), and 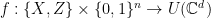 . For
. For 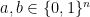 let
let  ,
,  , and assume
, and assume 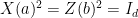 for all
for all  (we call such operators, unitaries with eigenvalues in
(we call such operators, unitaries with eigenvalues in 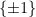 , observables). Suppose that the following inequalities hold: consistency
, observables). Suppose that the following inequalities hold: consistency
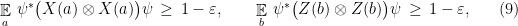
linearity
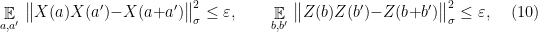
and anti-commutation
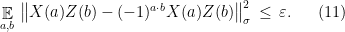
Then there exists a  , an isometry
, an isometry 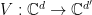 , and a representation
, and a representation 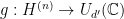 such that
such that  and
and
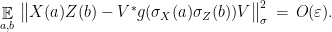
Note that the conditions (10) and (11) in the corollary are very similar to the conditions required of an approximate representation of the group 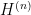 ; in fact it is easy to convince oneself that their exact analogue suffice to imply all the group relations. The reason for including only those relations is that they are the ones that it will be possible to test; see the next section for this. Condition (9) is necessary to derive the conditions of Theorem 4 from (10) and (11), and is also testable; see the proof.
; in fact it is easy to convince oneself that their exact analogue suffice to imply all the group relations. The reason for including only those relations is that they are the ones that it will be possible to test; see the next section for this. Condition (9) is necessary to derive the conditions of Theorem 4 from (10) and (11), and is also testable; see the proof.
Proof: To apply Theorem 4 we need to construct an 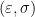 -representation
-representation  of the group
of the group 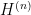 . Using that any element of
. Using that any element of 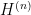 has a unique representative of the form
has a unique representative of the form  for
for 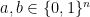 , we define
, we define  . Next we need to verify (3). Let
. Next we need to verify (3). Let  be such that
be such that 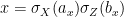 and
and 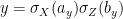 for
for  -bit strings
-bit strings  and
and  respectively. Up to phase, we can exploit successive cancellations to decompose
respectively. Up to phase, we can exploit successive cancellations to decompose  as
as
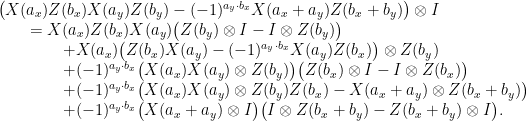
(It is worth staring at this sequence of equations for a little bit. In particular, note the “player-switching” that takes place in the 2nd, 4th and 6th lines; this is used as a means to “commute” the appropriate unitaries, and is the reason for including (9) among the assumptions of the corollary.) Evaluating each term on the vector 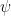 , taking the squared Euclidean norm, and then the expectation over uniformly random
, taking the squared Euclidean norm, and then the expectation over uniformly random  , the inequality
, the inequality  and the assumptions of the theorem let us bound the overlap of each term in the resulting summation by
and the assumptions of the theorem let us bound the overlap of each term in the resulting summation by 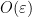 . Using
. Using 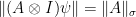 by definition, we obtain the bound
by definition, we obtain the bound
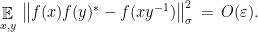
We are thus in a position to apply Theorem 4, which gives an isometry 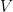 and exact representation
and exact representation 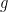 such that
such that
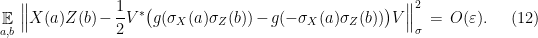
Using that 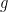 is a representation,
is a representation, 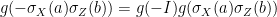 . It follows from (12) that
. It follows from (12) that 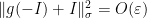 , so we may restrict the range of
, so we may restrict the range of 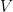 to the subspace where
to the subspace where 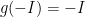 without introducing much additional error.
without introducing much additional error. 
3. Entanglement testing
Our discussion so far has barely touched upon the notion of entanglement. Recall the Schmidt decopmosition (7) of a unit vector 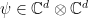 , and the associated reduced density matrix
, and the associated reduced density matrix  defined in (8). The state
defined in (8). The state 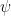 is called entangled if this matrix has rank larger than
is called entangled if this matrix has rank larger than  ; equivalently, if there is more than one non-zero coefficient
; equivalently, if there is more than one non-zero coefficient 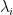 in (7). The Schmidt rank of
in (7). The Schmidt rank of 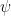 is the rank of
is the rank of  , the number of non-zero terms in (7). It is a crude, but convenient, measure of entanglement; in particular it provides a lower bound on the local dimension
, the number of non-zero terms in (7). It is a crude, but convenient, measure of entanglement; in particular it provides a lower bound on the local dimension  . A useful observation is that the Schmidt rank is invariant under local unitary operations: these may affect the Schmidt vectors
. A useful observation is that the Schmidt rank is invariant under local unitary operations: these may affect the Schmidt vectors 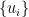 and
and 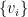 , but not the number of non-zero terms.
, but not the number of non-zero terms.
3.1. A certificate for high-dimensional entanglement
Among all entangled states in dimension  , the maximally entangled state
, the maximally entangled state  is the one which maximizes entanglement entropy, defined as the Shannon entropy of the distribution induced by the squares of the Schmidt coefficients:
is the one which maximizes entanglement entropy, defined as the Shannon entropy of the distribution induced by the squares of the Schmidt coefficients:
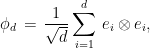
with entropy 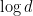 . The following lemma gives a “robust” characterization of the maximally entangled state in dimension
. The following lemma gives a “robust” characterization of the maximally entangled state in dimension  as the unique common eigenvalue-
as the unique common eigenvalue- eigenvector of all operators of the form
eigenvector of all operators of the form 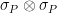 , where
, where 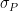 ranges over the elements of the unique
ranges over the elements of the unique  -dimensional irreducible representation of the Weyl-Heisenberg group
-dimensional irreducible representation of the Weyl-Heisenberg group 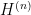 , i.e. the Pauli matrices (taken modulo
, i.e. the Pauli matrices (taken modulo 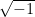 ).
).
Lemma 6 Let  ,
,  an integer,
an integer,  , and
, and  a unit vector such that
a unit vector such that
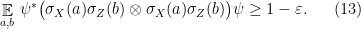
Then 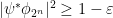 . In particular,
. In particular, 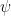 has Schmidt rank at least
has Schmidt rank at least  .
.
Proof: Consider the case 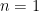 . The “swap” matrix
. The “swap” matrix
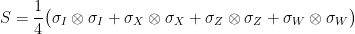
squares to identity and has a unique eigenvalue- eigenvector, the vector
eigenvector, the vector 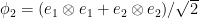 (a.k.a. “EPR pair”). Thus
(a.k.a. “EPR pair”). Thus 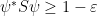 implies
implies 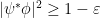 . The same argument for general
. The same argument for general  shows
shows  . Any unit vector
. Any unit vector  of Schmidt rank at most
of Schmidt rank at most  satisfies
satisfies  , concluding the proof.
, concluding the proof. 
Lemma 6 provides an “experimental road-map” for establishing that a bipartite system is in a highly entangled state:
- (i) Select a random
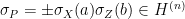 ;
;
- (ii) Measure both halves of
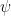 using
using 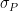 ;
;
- (iii) Check that the outcomes agree.
To explain the connection between the above “operational test” and the lemma I should review what a measurement in quantum mechanics is. For our purposes it is enough to talk about binary measurements (i.e. measurements with two outcomes, 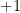 and
and 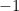 ). Any such measurement is specified by a pair of orthogonal projections,
). Any such measurement is specified by a pair of orthogonal projections, 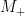 and
and 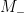 , on
, on 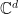 such that
such that  . The probability of obtaining outcome
. The probability of obtaining outcome 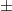 when measuring
when measuring 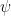 is
is 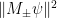 . We can represent a binary measurement succinctly through the observable
. We can represent a binary measurement succinctly through the observable  . (In general, an observable is a Hermitian matrix which squares to identity.) It is then the case that if an observable
. (In general, an observable is a Hermitian matrix which squares to identity.) It is then the case that if an observable 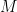 is applied on the first half of a state
is applied on the first half of a state  , and another observable
, and another observable  is applied on the second half, then the probability of agreement, minus the probability of disagreement, between the outcomes obtained is precisely
is applied on the second half, then the probability of agreement, minus the probability of disagreement, between the outcomes obtained is precisely  , a number which lies in
, a number which lies in ![{[-1,1]}](https://s0.wp.com/latex.php?latex=%7B%5B-1%2C1%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Thus the condition that the test described above accepts with probability
. Thus the condition that the test described above accepts with probability 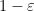 when performed on a state
when performed on a state 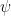 is precisely equivalent to the assumption (13) of Lemma 6.
is precisely equivalent to the assumption (13) of Lemma 6.
Even though this provides a perfectly fine test for entanglement in principle, practitioners in the foundations of quantum mechanics know all too well that their opponents — e.g. “quantum-skeptics” — will not be satisfied with such an experiment. In particular, who is to guarantee that the measurement performed in step (ii) is really 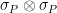 , as claimed? To the least, doesn’t this already implicitly assume that the measured system has dimension
, as claimed? To the least, doesn’t this already implicitly assume that the measured system has dimension  ?
?
This is where the notion of device independence comes in. Briefly, in this context the idea is to obtain the same conclusion (a certificate of high-dimensional entanglement) without any assumption on the measurement performed: the only information to be trusted is classical data (statistics generated by the experiment), but not the operational details of the experiment itself.
This is where Corollary 5 enters the picture. Reformulated in the present context, the corollary provides a means to verify that arbitrary measurements “all but behave” as Pauli measurements, provided they generate the right statistics. To explain how this can be done we need to provide additional “operational tests” that can be used to certify the assumptions of the corollary.
3.2. Testing the Weyl-Heisenberg group relations
Corollary 5 makes three assumptions about the observables 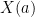 and
and  : that they satisfy approximate consistency (9), linearity (10), and anti-commutation (11). In this section I will describe two (somewhat well-known) tests that allow to certify these relations based only on the fact that the measurements generate statistics which pass the tests.
: that they satisfy approximate consistency (9), linearity (10), and anti-commutation (11). In this section I will describe two (somewhat well-known) tests that allow to certify these relations based only on the fact that the measurements generate statistics which pass the tests.
Linearity test:
- (a) The referee selects
 and
and 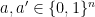 uniformly at random. He sends
uniformly at random. He sends 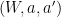 to one player and
to one player and 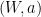 ,
, 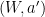 , or
, or  to the other.
to the other.
- (b) The first player replies with two bits, and the second with a single bit. The referee accepts if and only if the player’s answers are consistent.
As always in this note, the test treats both players simultaneously. As a result we can (and will) assume that the player’s strategy is symmetric, and is specified by a permutation-invariant state  and a measurement for each question: an observable
and a measurement for each question: an observable  associated to questions of the form
associated to questions of the form 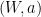 , and a more complicated four-outcome measurement
, and a more complicated four-outcome measurement 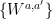 associated with questions of the form
associated with questions of the form 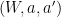 (It will not be necessary to go into the details of the formalism for such measurements).
(It will not be necessary to go into the details of the formalism for such measurements).
The linearity test described above is exactly identical to the BLR linearity test described earlier, but for the use of the basis label  . The lemma below is a direct analogue of Lemma 1, which extends the analysis to the setting of players sharing entanglement. The lemma was first introduced in a joint paper with Ito, where we used an extension of the linearity test, Babai et al.’s multilinearity test, to show the inclusion of complexity classes NEXP
. The lemma below is a direct analogue of Lemma 1, which extends the analysis to the setting of players sharing entanglement. The lemma was first introduced in a joint paper with Ito, where we used an extension of the linearity test, Babai et al.’s multilinearity test, to show the inclusion of complexity classes NEXP MIP
MIP .
.
Lemma 7 Suppose that a family of observables  for
for  and
and  , generates outcomes that succeed in the linearity test with probability
, generates outcomes that succeed in the linearity test with probability 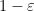 , when applied on a bipartite state
, when applied on a bipartite state 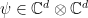 . Then the following hold: approximate consistency
. Then the following hold: approximate consistency

and linearity
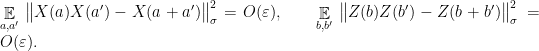
Testing anti-commutation is slightly more involved. We will achieve this by using a two-player game called the Magic Square game. This is a fascinating game, but just as for the linearity test I will treat it superficially and only recall the part of the analysis that is useful for us (see e.g. the paper by Wu et al. for a description of the game and a proof of Lemma 8 below).
Lemma 8 (Magic Square) The Magic Square game is a two-player game with nine possible questions (with binary answers) for one player and six possible questions (with two-bit answers) for the other player which has the following properties. The distribution on questions in the game is uniform. Two of the questions to the first player are labelled  and
and  respectively. For any strategy for the players that succeeds in the game with probability at least
respectively. For any strategy for the players that succeeds in the game with probability at least 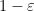 using a bipartite state
using a bipartite state 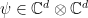 and observables
and observables  and
and  for questions
for questions  and
and  respectively, it holds that
respectively, it holds that
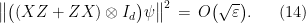
Moreover, there exists a strategy which succeeds with probability  in the game, using
in the game, using  and Pauli observables
and Pauli observables 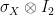 and
and  for questions
for questions  and
and  respectively.
respectively.
Based on the Magic Square game we devise the following “anti-commutation test”.
Anti-commutation test:
- (a) The referee selects
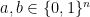 uniformly at random under the condition that
uniformly at random under the condition that 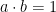 . He plays the Magic Square game with both players, with the following modifications: if the question to the first player is
. He plays the Magic Square game with both players, with the following modifications: if the question to the first player is  or
or  he sends
he sends  or
or  instead; in all other cases he sends the original label of the question in the Magic Square game together with both strings
instead; in all other cases he sends the original label of the question in the Magic Square game together with both strings  and
and  .
.
- (b) Each player provides answers as in the Magic Square game. The referee accepts if and only if the player’s answers would have been accepted in the game.
Using Lemma 8 it is straightforward to show the following.
Lemma 9 Suppose a strategy for the players succeeds in the anti-commutation test with probability at least 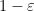 , when performed on a bipartite state
, when performed on a bipartite state 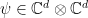 . Then the observables
. Then the observables 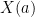 and
and  applied by the player upon receipt of questions
applied by the player upon receipt of questions  and
and  respectively satisfy
respectively satisfy
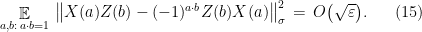
3.3. A robust test for high-dimensional entangled states
We are ready to state, and prove, our main theorem: a test for high-dimensional entanglement that is “robust”, meaning that success probabilities that are a constant close to the optimal value suffice to certify that the underlying state is within a constant distance from the target state — in this case, a tensor product of  EPR pairs. Although arguably a direct “quantization” of the BLR result, this is the first test known which achieves constant robustness — all previous
EPR pairs. Although arguably a direct “quantization” of the BLR result, this is the first test known which achieves constant robustness — all previous  -qubit tests required success that is inverse polynomially (in
-qubit tests required success that is inverse polynomially (in  ) close to the optimum in order to provide any meaningful conclusion.
) close to the optimum in order to provide any meaningful conclusion.
 -qubit Pauli braiding test: With probability
-qubit Pauli braiding test: With probability 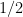 each,
each,
- (a) Execute the linearity test.
- (b) Execute the anti-commutation test.
Theorem 10 Suppose that a family of observables  , for
, for  and
and  , and a state
, and a state  , generate outcomes that pass the
, generate outcomes that pass the  -qubit Pauli braiding test with probability at least
-qubit Pauli braiding test with probability at least 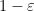 . Then
. Then 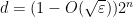 .
.
As should be apparent from the proof it is possible to state a stronger conclusion for the theorem, which includes a characterization of the observables  and the state
and the state 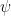 up to local isometries. For simplicity I only recorded the consequence on the dimension of
up to local isometries. For simplicity I only recorded the consequence on the dimension of 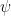 .
.
Proof: Using Lemma 7 and Lemma 9, success with probability 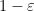 in the test implies that conditions (9), (10) and (11) in Corollary 5 are all satisfied, up to error
in the test implies that conditions (9), (10) and (11) in Corollary 5 are all satisfied, up to error 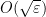 . (In fact, Lemma 9 only implies (11) for strings
. (In fact, Lemma 9 only implies (11) for strings  such that
such that 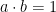 . The condition for string such that
. The condition for string such that 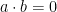 follows from the other conditions.) The conclusion of the corollary is that there exists an isometry
follows from the other conditions.) The conclusion of the corollary is that there exists an isometry 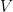 such that the observables
such that the observables 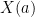 and
and  satisfy
satisfy
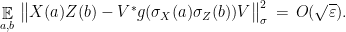
Using again the consistency relations (9) that follow from part (a) of the test together with the above we get
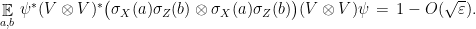
Applying Lemma 6,  has Schmidt rank at least
has Schmidt rank at least  . But
. But  is a local isometry, which cannot increase the Schmidt rank.
is a local isometry, which cannot increase the Schmidt rank.